This example demonstrates how to model and simulate Linear and Logarithmic chirp signals. Chirp signals are widely used in radar pulse compression, audio equipment testing, and system identification to measure frequency response over a wide band in a single sweep.
Theoretical Basis
Linear Chirp
The instantaneous frequency increases linearly with time.
Frequency:
Where is the sweep rate (Hz/s) and is the start frequency.
Time Domain Signal:
Logarithmic Chirp
The instantaneous frequency increases exponentially, which matches human pitch perception (octaves).
Frequency:
Time Domain Signal:
Simulation Models
Linear Chirp Model
To build this in Simit:
- Source: Use a Ramp block to generate time (or use simulation time).
- Math: Implement the phase equation .
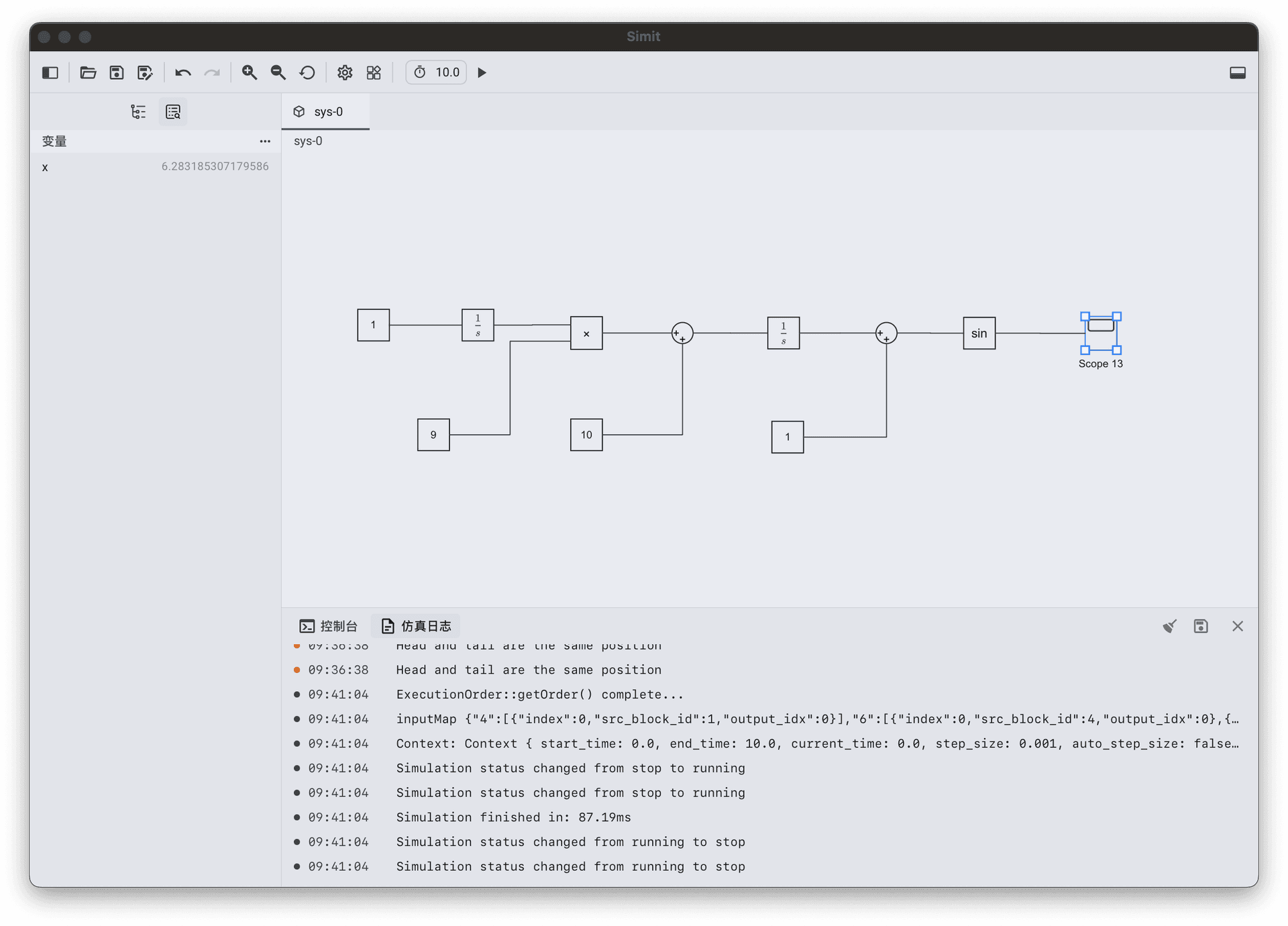
Parameters:
| Parameter | Symbol | Value | Description |
|---|---|---|---|
| Start Freq | 9 Hz | Initial frequency | |
| Sweep Rate | 10 Hz/s | Frequency increment per second | |
| Amplitude | Signal amplitude | ||
| Sample Time |
Logarithmic Chirp Model
Parameters:
| Parameter | Symbol | Value | Description |
|---|---|---|---|
| Angular Freq | Base angular frequency | ||
| Log Coeff | 0.1 | Controls exponential curvature | |
| Amplitude | 10 | Peak amplitude |
Results Analysis
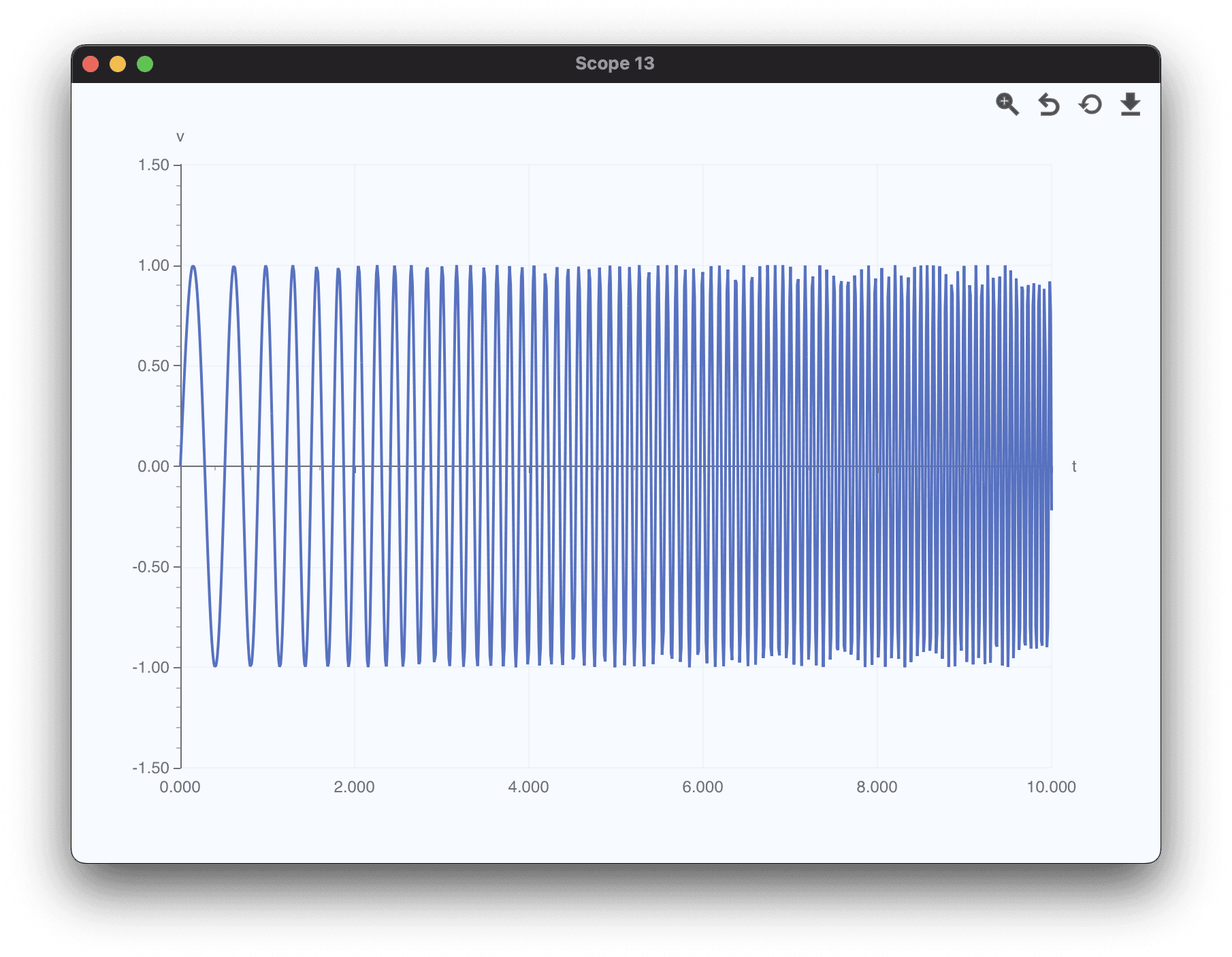
Linear Sweep
- Uniform Compression: The waveform cycles get shorter at a constant rate.
- Verification: At , frequency . Period .
Logarithmic Sweep
- Exponential Compression: Cycles are sparse at first but compress rapidly later.
- Dynamic Range: Covers a wide frequency range quickly, ideal for Bode plot analysis.
Applications
- Radar: Pulse compression for high range resolution.
- Audio: Measuring speaker frequency response (Log Chirp matches hearing).
- Vibration: Modal analysis of mechanical structures.