This example demonstrates how to build a transfer function-based DC motor speed closed-loop control system, employing feedforward compensation and anti-windup PID control strategies to achieve high-precision, fast-response motor speed regulation.
The system uses a dual-channel drive architecture to eliminate steady-state error while ensuring dynamic performance.
Theoretical Basis
DC Motor Transfer Function Modeling
A DC motor is composed of an armature circuit coupled with a mechanical rotating subsystem.
Armature Circuit Voltage Equation:
Mechanical Torque Balance Equation:
Where is the drive voltage, is the rotor angular velocity, is the torque constant, is the back-EMF constant, is the moment of inertia, and is the friction coefficient.
Transfer Function Derivation: Eliminating the current variable yields the standard second-order form:
Feedforward + PID Dual-Channel Control
The system adopts a parallel drive structure, balancing response speed and disturbance rejection.
Feedforward Channel:
Directly generates the baseline drive voltage based on the reference speed, achieving fast response without overshoot.
PID Channel:
Compensates for model errors and external disturbances through Proportional-Integral-Derivative regulation.
Total Control Output:
Anti-Windup Mechanism
When the control voltage exceeds the saturation limit, the anti-windup loop is activated to suppress integrator saturation:
Simulation Model
Model Hierarchy
The system uses a modular design, as shown below:
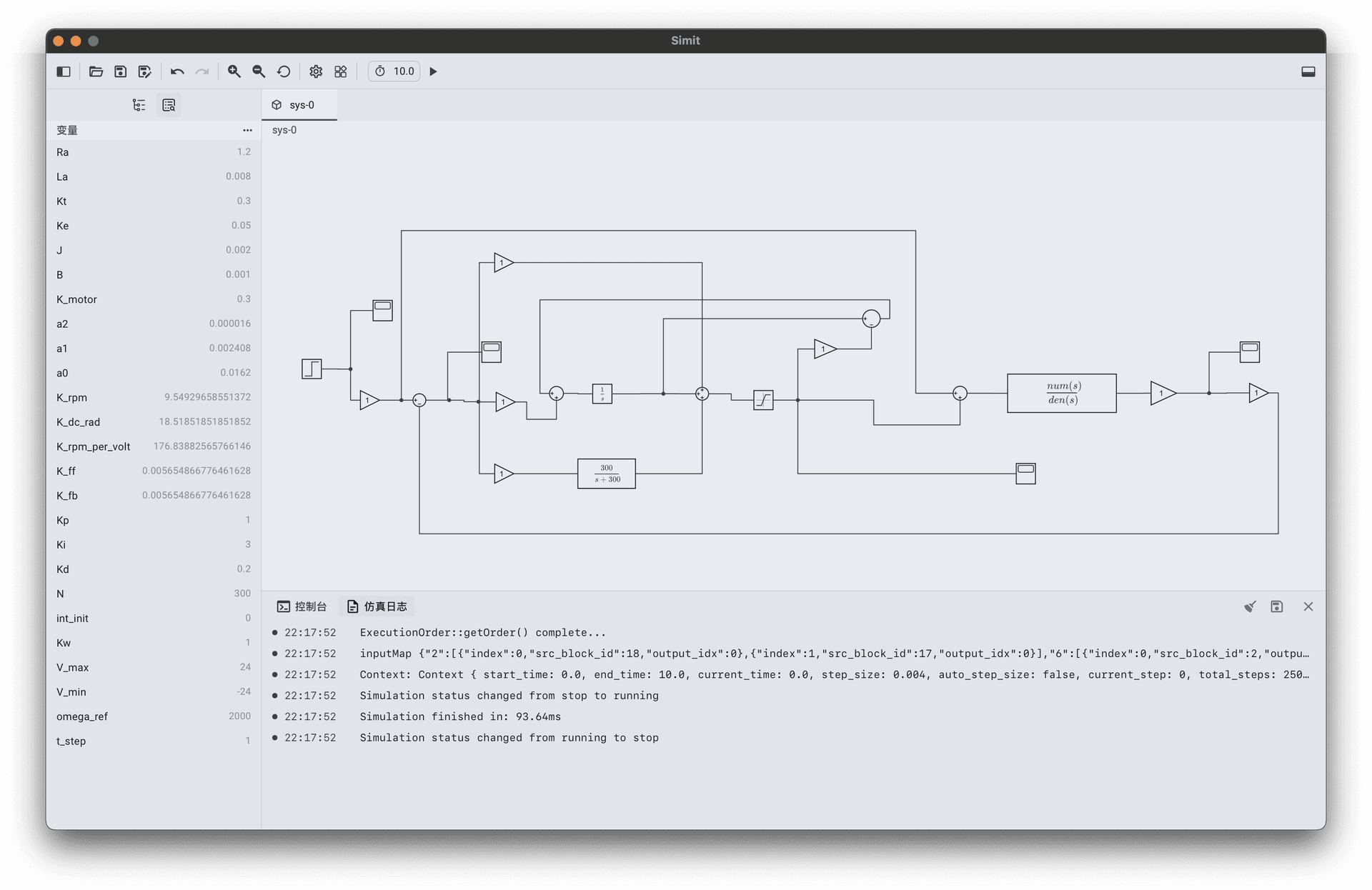
Core Block Parameter Quick Reference
| Block Function | Parameter | Value | Description |
|---|---|---|---|
| Target Speed | omega_ref | 2000 | Target Speed (rpm) |
t_step | 1.0 | Step Time (s) | |
| Motor TF | Kt | 0.3 | Torque Constant (N·m/A) |
Ke | 0.05 | Back-EMF Constant (V/(rad/s)) | |
Ra | 1.2 | Armature Resistance (Ω) | |
La | 0.008 |
Note: K_rpm_per_volt = Kt / (Ra*B + Kt*Ke) * 60/(2*pi) is the DC gain of the motor (rpm/V), automatically calculated from raw parameters.
Performance Metrics
Steady-State Performance
- Steady-State Error: ≤ 1% × Target Speed
- Target: 2000, Steady-State: 2004
- Voltage Utilization: ≤ 70% (Reserved dynamic margin)
- Limit: 24V, Max Control Voltage: ~13V
Dynamic Performance
- Overshoot: ≤ 5%
- Settling Time: ≤ 1.5s (Within ±2% error band)
- Anti-Windup Recovery: ≤ 0.3s
Results Analysis
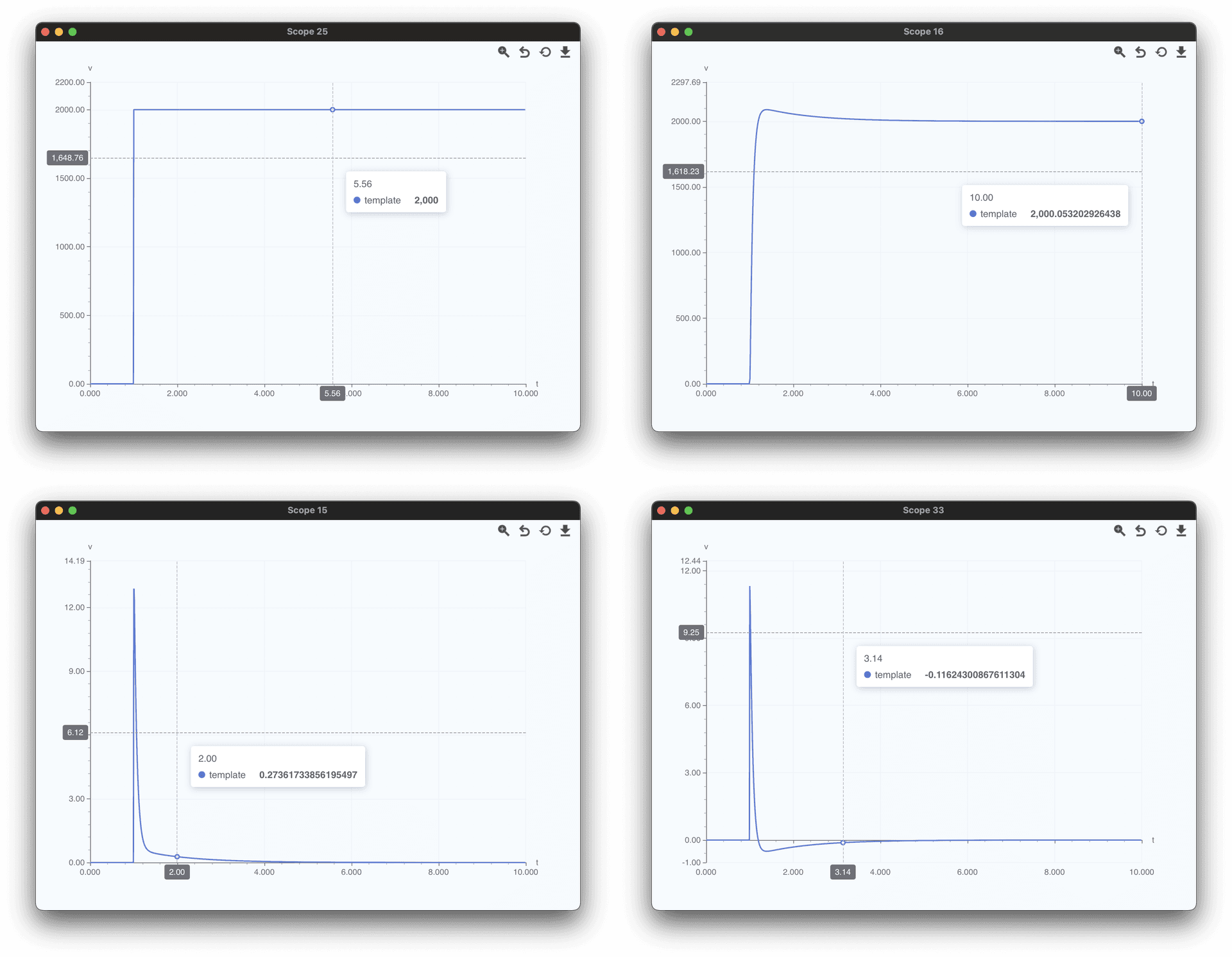
Typical Response Process:
- 0-0.2s: Feedforward channel dominates, approaching target speed rapidly.
- 0.2-1.0s: PID channel fine-tunes, integrator eliminates residual error.
- >1.5s: Enters steady state, PID output approaches zero, feedforward maintains speed.
Observed Effects:
- Speed tracks the setpoint smoothly with static error < 10 rpm.
- Voltage output is smooth with no significant saturation.
- Anti-windup mechanism intervenes quickly during load steps.
Applications
- Engineering Prototyping: Development of 24V DC motor speed control systems.
- Algorithm Research: PID parameter auto-tuning, intelligent anti-windup strategies.
Configuration Code
# 1 Motor Physical Parameters (SI Units)
# Modify these parameters to adapt to different motors
Ra = 1.2; # Armature Resistance (Ω) - Affects steady-state voltage demand
La = 0.008; # Armature Inductance (H) - Affects electrical response speed
Kt = 0.3; # Torque Constant (N·m/A) - Affects torque output capability
Ke = 0.05; # Back-EMF Constant (V/(rad/s)) - Key: Smaller Ke means higher max speed
J = 0.002; # Moment of Inertia (kg·m²) - Affects mechanical response speed
B = 0.001; # Friction Coefficient (N·m/(rad/s)) - Affects low-speed performance
# 2 Transfer Function Coefficient Calculation
# Automatically calculate numerator and denominator based on physical parameters
K_motor = Kt; # TF Numerator = Torque Constant
a2 = La * J; # 2nd-order term: Electro-mechanical coupling
a1 = Ra * J